This calculator can be used to convert decimal numbers to a binary floating point number in IEEE-754 format or vice versa.
Floating point numbers in the IEEE-754 representation have a fixed number of bits (usually 32 or 64). They can be used to represent both very large and very small numbers. However, numbers with decimal places in particular often cannot be represented exactly, which is why rounding is often necessary.
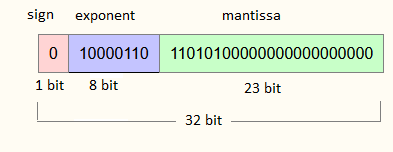
Binary numbers in IEEE-754 representation start with a sign bit. This is followed by exponent bits and this is followed by a mantissa. For example, a binary floating point number with 32 bits has 1 sign bit, 8 bits for the exponent and 23 bits for the mantissa.
Formats
There are several formats in which floating point numbers can be represented. These differ in the total number of bits and in the number of bits for the exponent and the mantissa. Furthermore, they differ in a so-called bias value, which is used to store negative exponents without an additional sign bit.
| data type | size | exponent | mantissa | bias |
|---|---|---|---|---|
| binary16 | 16 bits | 5 bits | 10 bits | 15 |
| binary32 | 32 bits | 8 bits | 23 bits | 127 |
| binary64 | 64 bits | 11 bits | 52 bits | 1023 |
| binary128 | 128 bits | 15 bits | 112 bits | 16383 |
The more bits the mantissa has, the more precisely a number can be represented.
Special values
| value | sign | exponent | mantissa |
|---|---|---|---|
| 0 | 0 or 1 | 00000000 | 00000000000000000000000 |
| ∞ | 0 | 11111111 | 00000000000000000000000 |
| −∞ | 1 | 11111111 | 00000000000000000000000 |
| denormalized | 0 or 1 | 00000000 | arbitrary, but not only zeros |
| NaN | 0 or 1 | 11111111 | arbitrary, but not only zeros |
Convert decimal number to floating point number
A decimal number can be converted to IEEE-754 floating point representation using the following steps:
- determine sign bit
- convert number to binary
- shift point so that there is only one 1 in front of the point
- round
- add bias to the exponent value
- convert exponent to the binary system
- assemble floating point number
To illustrate the procedure, the number -42.625 is to be represented as a binary floating point number in the binary32 format.
1. determine sign bit:
If the number is positive, a 0 is written in the sign bit, and if it is negative, a 1 is written.
-42.625 is negative. Thus, the sign bit is 1.
2. convert number to binary:
Next, the 42.625 must be converted into a binary number. You get: 101010.1012
This can also be written as follows: 101010.1012 ∙ 20
3. shift point so that there is only one 1 in front of the point:
The binary point must be shifted in such a way that there is exactly one 1 before the binary point and nothing else. The exponent is adjusted accordingly.
The binary point is shifted 5 places to the left. It applies:: 101010.1012 ∙ 20 = 1.010101012 ∙ 25
Note: If the point had been moved to the right, the exponent would have become negative.
4. round:
If large numbers or numbers containing a binary point are to be converted into an IEEE-754 floating point number, it can happen that not all digits after the binary point fit into the mantissa. In this case, the number must be rounded so that it has a maximum of as many fractional digits as the mantissa has bits. There are different possibilities to round. Among others, it is possible to always round up, always round down or always round towards 0. All 3 methods have the disadvantage that with long calculations, with which always in the same direction is rounded, the rounding error increases further and further.
There is a fourth variant which is usually chosen. According to this variant, the number is always rounded to the next representable number. So if the number is closer to the next smaller number than to the next larger one, it is rounded down (and vice versa). If the number is exactly in the middle between the next smaller and the next larger number, then it is rounded to the number that has a 0 in the last bit of the mantissa. From a statistical point of view, the number is rounded up as often as it is rounded down, and this reduces the problem with the ever-increasing rounding error.
If a number is according to amount too large to be displayed (the exponent is larger than the bias before the bias is included), it is rounded to ∞ or to −∞.
1.010101012 has 8 fractional digits and 23 bits fit into the mantissa. This means that rounding is not necessary.
5. add bias to the exponent value:
Next, the bias must be added to the value of the exponent. For floating point numbers with 32 bits, the bias is 127. So we calculate: 5 + 127 = 132
6. convert exponent to the binary system:
Then, the exponent value to which the bias was added is converted into a binary number.
13210 ≙ 100001002
7. assemble floating point number:
Now everything is put together. The value determined in step 1 goes into the sign bit. The binary number calculated in step 6 is placed in the exponent part. If this would not fill the exponent part completely, then the binary number would be extended by leading zeros.
The bits after the point are written in the mantissa. The 1 before the binary point is discarded. If the mantissa is not completely filled by the fractional digits, zeros are appended until the bit number for the mantissa is reached. If there are more fractional digits than bits are provided for the mantissa, rounding is required.
A "1" is entered in the sign bit.
The "10000100" determined in step 6 belongs in the exponent part.
The fractional digits "01010101" determined in step 3 belong to the mantissa. Since there are only 8 fractional digits, 15 zeros must be added to get the required 23 bits.
The result is:
Convert floating point number to decimal number
A binary floating point number in IEEE-754 format can be converted to a decimal number using the following steps:
- convert exponent to decimal
- subtract bias from the exponent
- extend mantissa by leading "1."
- shift point
- convert mantissa to decimal number
- determine sign
As an example, the following number is to be converted to the decimal system:
1. convert exponent to decimal:
First, the exponent part is converted from the binary system to the decimal system.
100001002 ≙ 13210
2. subtract bias from the exponent:
Then the bias (in this case 127) is subtracted from the exponent.
132 - 127 = 5
3. extend mantissa by leading "1.":
Then the mantissa is extended by "1.": 1.10111001000000000000000
4. shift point:
Next, the binary point must be shifted so that the exponent becomes 0. If the exponent is greater than 0, the point must be moved to the right, otherwise to the left.
1.101110012 ∙ 25 = 110111.0012 ∙ 20
5. convert mantissa to decimal number:
The result will now be converted to the decimal system:
110111.0012 ≙ 55.12510
6. determine sign:
If the sign bit is a 1, a minus sign is written in front of the number, otherwise the number is positive.
The sign bit is 0. So the result is positive and the result is 55.125.
Hexadecimal notation
For better readability floating point numbers are often not displayed in binary notation but in hexadecimal notation. For this purpose, the binary number is divided into 4-bit blocks and each block is combined into a hexadecimal character.
For example, 0x4208EC8B is much shorter than "01000010000010001110110001011". The "0x" in front of the number means that the number is a hexadecimal number.
Denormalized numbers
When converting a number into a floating point number, the binary point may be shifted to the right by a maximum of bias − 1 places. This means that numbers that are very close to 0 cannot be represented in a normalized form. In this case, the binary point is shifted to the right by exactly bias − 1 places. Then there is a 0 before the binary point instead of a 1. The number is then rounded and the fractional digits are entered in the mantissa as usual. There are only zeros in the exponent. This method can be used to represent numbers as floating point numbers that would otherwise not be representable.
When converting the denormalized floating point number back into a decimal number, the mantissa is extended by "0." instead of "1." and then the binary point is shifted to the left by exactly bias − 1.