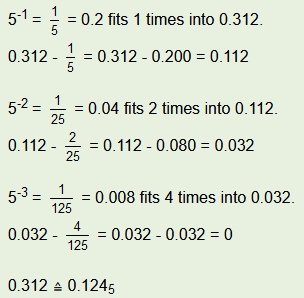This calculator can be used to convert numbers from one numeral system to a numeral system with a different base.
Conversion to decimal system
To convert a number from a numeral system with any base b to the decimal system (base 10), the last digit must be multiplied by b0, the second to last digit by b1, the third from last digit by b2, etc. and after that you have to sum up the results.
Assuming the number 31645 is to be converted from the 5s system to the decimal system. Then you calculate:
| 31245 | ≙ | 3 ∙ 53 + 1 ∙ 52 + 2 ∙ 51 + 4 ∙ 50 |
| = | 3 ∙ 125 + 1 ∙ 25 + 2 ∙ 5 + 4 ∙ 1 | |
| = | 375 + 25 + 10 + 4 | |
| = | 414 |
convert numbers with fractional places:
If the number to be converted to the decimal system is a has fractional places, the procedure for the digits before the point is as described above. For the decimal places, the first digit after the point is multiplied by b-1, the second by b-2, the third by b-3 etc.. The sum of the results is formed and added to what was received for the digits before the point.
As an example, the number 3.1245 is to be converted from the 5s system to the decimal system:
| 3.1245 | ≙ | 3 ∙ 50 + 1 ∙ 5-1 + 2 ∙ 5-2 + 4 ∙ 5-3 | ||||||
| = | 3 ∙ 1 +
|
|||||||
| = | 3 +
|
|||||||
| = | 3 + 0.2 + 0.08 + 0.032 | |||||||
| = | 3.312 |
Convert from decimal system to other numeral system
There are several methods for converting a number from the decimal system to a numeral system with a different base b. This can be achieved either by repeatedly dividing by the base or with the help of powers of the base.
divide by base:
With this method the number is divided with remainder by the base b. The remainder is memorized and the integer part of the result is again divided by b with remainder. This is done until the integer part of the result is 0.
As an example, the number 414 is to be converted from the decimal system to the 5s system.
| 414 | : | 5 | = | 82 | R | 4 |
| 82 | : | 5 | = | 16 | R | 2 |
| 16 | : | 5 | = | 3 | R | 1 |
| 3 | : | 5 | = | 0 | R | 3 |
Now the result is built by the remainders read from the bottom to the top. Thus it results in the example that 414 in the decimal system corresponds to 3124 in the 5s system.
Base from target numeral system greater than 10:
If the base of the numeral system into which the number is to be converted is greater than 10, it is possible that the remainder will result in a number greater than 9. In this case, not the number is appended to the result, but the character that represents this number. For example, in the 16s system, instead of a 10 an A is appended, instead of an 11 a B is appended, instead of a 12 a C is appended, instead of a 13 a D is appended, instead of a 14 an E is appended, and instead of a 15 an F is appended.
As an example, 6010 is to be converted to the 16 system.
| 60 | : | 16 | = | 3 | R | 12 |
| 3 | : | 16 | = | 0 | R | 3 |
The 12 is greater than 9 and must therefore be converted to the character that represents the 12. This is C.
Thus 6010 in the decimal system corresponds to 3C16 in the hexadecimal system.
Conversion of numbers with decimal point:
As an example, the number 7.56 is to be converted into the 5 system. To convert a number with a decimal point from the decimal system into a numeral system with a different base, the number must first be divided into an integer part and a fractional part. The 7.56 is thus divided into 7 and 0.56. First, the 7 is converted into the 5 system as described above. 710 ≙ 125.
Next, the decimal places are to be converted. To do this, multiply the fractional part by the base (in this case 5). From the result, the part before the decimal point is appended to the solution and the part after the decimal point is multiplied by the base again. This is done until the result of the mulitplication is an integer.
| 0.56 | ∙ | 5 | = | 2.80 |
| 0.8 | ∙ | 5 | = | 4.0 |
Now only the converted digits before and after the decimal point have to be appended to each other:
With powers:
To show how numbers are converted from the decimal system to a numeral system with a different base with the help of powers, we will again convert the 414 from the 10s system to the 5s system.
First, find the largest power of 5 that is less than or equal to 414. That is 53 = 125.
The next step is to determine how many times the 125 fits into the 414. That is 3 times.
The 3 is now the first digit that you write into the result. Now multiply the 125 and the 3 and subtract the product from the 414. One receives thus: 414 - 3 ∙ 125 = 414 - 375 = 39
Next, determine how many times 52 = 25 fits into the 39. That is 1 times. So you append the 1 to the result and subtract 1 ∙ 25 from the 39.
Then you do the same with 51 = 5 and 50 = 1. The whole calculation path looks like this:
Convert decimal numbers with decimal point with powers:
As an example, the number 414,31210 is to be converted from the decimal system to the 5s system.
To convert a number with a decimal point from the decimal system to a numeral system with a different base b with the help of powers, the number must first be divided into an integer part and a fractional part. In the example, these are 414 and 0.312.
The integer part is converted to the 5s system as described above: 41410 ≙ 31245.
The conversion of the fractional part works very similar to the conversion of the integer part. This time, however, we first look at how often 5-1 = 0.2 fits into 0.312. These are 1 times. So the 1 is the first decimal place of the result and 0.312 - 1 ∙ 0.2 must be calculated. That is 0.112.
Next, it is calculated how many times 5-2 = 0.04 fits into the 0.112. Following this scheme, the calculation is continued until either the subtraction results in 0 or until the maximum number of decimal places to be calculated is reached. The entire calculation for the fractional part looks as follows:
If you now combine the results of the integer part and the fractional part, you get:
414.31210 ≙ 3124.1245
Basis of source and target numeral system arbitrary
In the above sections, either the source numeral system or the target numeral system always had base 10. If neither the source numeral system nor the target numeral system has base 10, the number is first converted from the source numeral system to the decimal system, and then the number is converted from the decimal system to the target numeral system.