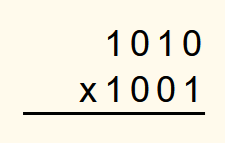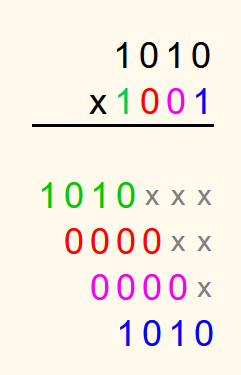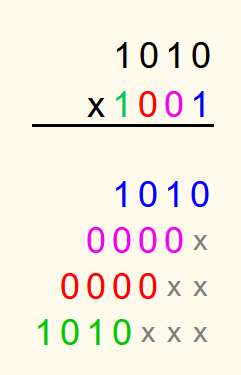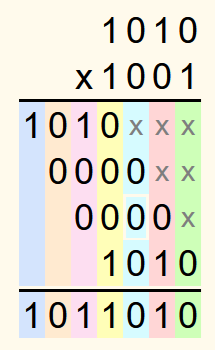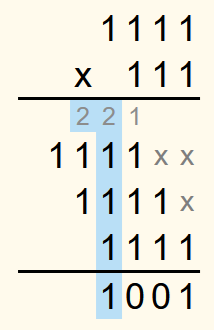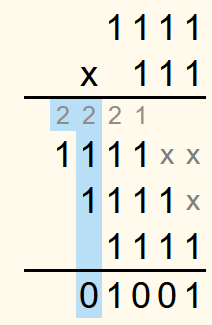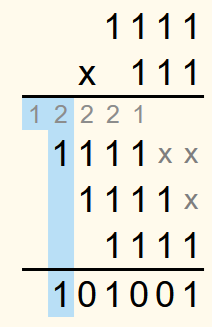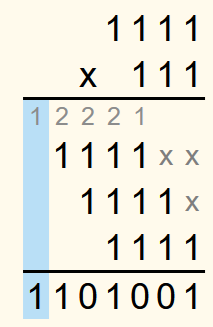About the calculator
This online calculator can be used to multiply 2 binary numbers. The numbers may be negative and contain a binary point.
Multiplying binary numbers
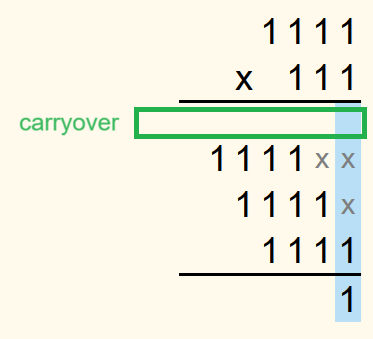
2 binary numbers are multiplied in the same way as 2 decimal numbers are multiplied. First, the two binary numbers to be multiplied are written down.
All digits of the second number are then multiplied by the first number and written underneath each other so that the number is shifted to the left by as many digits as there are places after the current digit in the second number. For better clarity, the empty spaces to the right of the numbers can be marked with an “x” or a dot. However, this is not necessary. If the current digit is a 0 and the product is therefore 0, then often as many zeros are written down as the first number has digits instead of just one 0.
It doesn't matter whether you start with the first or the last digit of the second number.
Then, starting from the right, for each column the sum of the numbers in this column is calculated. If the sum of a column is 0 or 1, it is written in the row for the solution.
Carryovers:
If the sum of the numbers in a column is greater than 1, then the last digit of the sum converted into a binary number is written in the row for the solution, and what comes before the last digit is written in the row for the carryovers one column to the left. The carryovers can be written down as binary numbers. However, when adding up the next column, it must be taken into account that the number in the row for the carryover is a binary number. It is simpler and more compact if the carryovers are written down as decimal numbers.
For example, if the sum of the numbers in a column is 3, the number is first converted into a binary number. This results in 112. The back 1 is written in the row for the solution and the front 1 in the row for the carryovers.
If the sum of the numbers in a column is 10, this results in 10102 when converted into a binary number. The trailing 0 is written in the row for the solution and 1012 is converted into a decimal number. This results in 5. And this 5 is written in the row for the carryovers one column to the left.
Example:
As an example, 11112 ∙ 1112 is to be calculated.
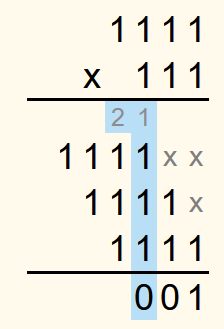
In the last column there is only one 1, so the 1 is written in the row for the solution.
The sum of the numbers in the second last row is 2. Converted into a binary number, this is 102. The 0 is written in the row for the solution and the 1 in the row for the carryovers one column to the left.
In the next column, the sum of the numbers is 4, which is 1002 in the binary system. The 0 is written in the row for the solution and because 102 is 2 in the decimal system, a 2 is written in the row for the carryovers.
In the fourth column from the right, the sum is 5, which corresponds to 1012. So a 1 is written in the row for the solutions and a 2 in the row for the carryovers.
In the next column, the sum is again 4 and therefore a 0 is written in the row for the solution and the carry is 2.
Then the sum is 3, which corresponds to 112. So a 1 is written in both the row for the solution and the row for the carryovers.
alternative calculation of the carryovers:
The sum of a column does not have to be converted into a binary number to determine the carryover and the number that is written in the row for the solution. Instead, the sum can also be divided by 2. If the sum is divisible by 2, then a 0 is written in the row for the solution, otherwise a 1. To determine the carryover, the sum is divided by 2 and rounded down.
For example, if the sum of the numbers in a column is 5, then a 1 is written in the row for the solutions because 5 is not divisible by 2. To calculate the carryover, 5 is divided by 2. This results in 2.5 and if you round the 2.5 down, you get 2.
Numbers with binary points:
If at least one of the two factors is a number with a binary point, each digit of the second number is multiplied by the first number in the same way as for binary numbers without a binary point. The binary points of the first number can be included, but they can also be omitted.
Then, as with the multiplication of binary numbers without binary points, the row for the solution and the row for the carryovers are calculated. When doing this, the binary points are not taken into account.
The binary point is placed in the solution so that the solution has as many places behind the binary point as the two factors together.