This calculator can be used to convert binary numbers to hexadecimal numbers and hexadecimal numbers to binary numbers.
If you want to convert a number from a number system with base a to a number system with base b, then you can first convert the number from the number system with base a to the decimal system and from the decimal system to the number system with base b. If you do this by hand, it can be very time-consuming for large numbers. But for the conversion from the binary system to the hexadecimal system or vice versa, there is a trick with which you can do the conversion very easily and without electronic tools. For this the following table can be helpful:
| hexadecimal | binary |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
| hexadecimal | binary |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| hexadecimal | binary |
|---|---|
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
Convert binary to hexadecimal
If you want to convert a binary number into a hexadecimal number, you divide the binary number into blocks. With the exception of the foremost block, all blocks must consist of exactly 4 bits. The foremost block can also contain less than 4 bits. If you want, you can fill it up with leading 0's, so that it also consists of 4 bits. After that you only have to convert each block into the hexadecimal system. With 4-bit blocks this can be done quite easily in your head or you can use a table like the one above. The order of the digits of the hexadecimal number corresponds to the order of the respective blocks of the binary number.
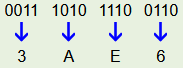
As an example, 111010111001102 is to be converted to the hexadecimal system.
In the hexadecimal system, the number is thus: 3AE616
binary in hexadecimal with binary point:
The same principle can be used to convert numbers with binary point from the binary system to the hexadecimal system. This time the blocks are divided in such a way that all blocks between the foremost block of the part before the pointand the rearmost block of the part behind the point contain exactly 4 bits. The two blocks on the outside may have less than 4 bits. Each block may only contain bits from either the part before the point or the part after the point. If the backmost block of the fractional part contains less than 4 bits, it is important to treat it as if it were filled up with zeros at the back. For example, if the last block of the fractional part contains only a "1", this block is treated as if there were a "1000". In order not to make a mistake, it can also be useful to write down the additional zeros.
As an example, the number 1110101110.0110012 is to be converted from the binary system to the hexadecimal system. One calculates:
In the hexadecimal system, the number is: 3AE,6416
convert hexadecimal to binary
If you want to convert a number from the hexadecimal system to the binary system, you just have to convert each digit of the hexadecimal number to the corresponding 4-bit block in the binary system. If the first block starts with zeros, these may be removed.
For example, 3A216 is to be converted to the binary system:
The first two zeros in the foremost block can be removed. The following therefore applies: 3A216 ≙ 11101000102
hexadecimal to binary with fractionals:
For numbers with point, proceed in principle as described above. However, if the last 4-bit block ends with zeros, these may be removed.
As an example, 5.A4816 is to be converted to binary. Thus one calculates:
The last 3 zeros can be removed. So it applies: 5.A4816 ≙ 101.1010010012