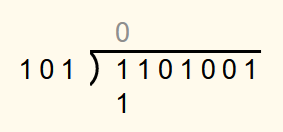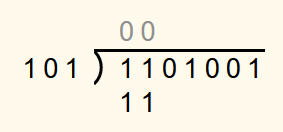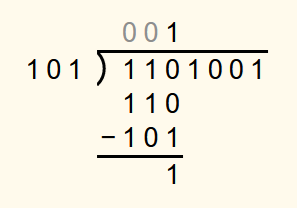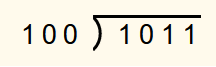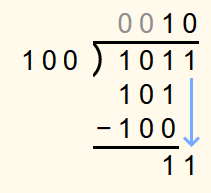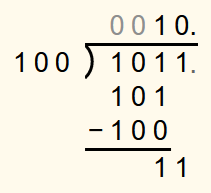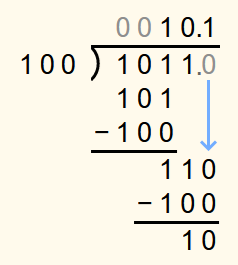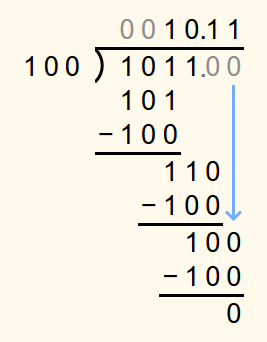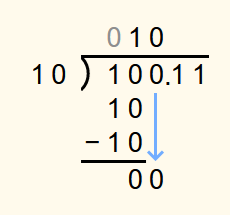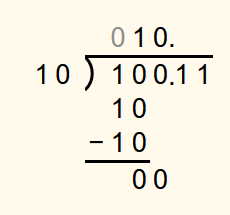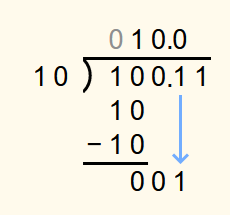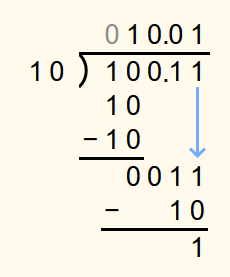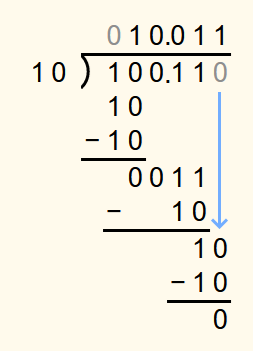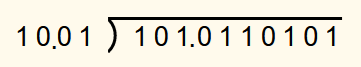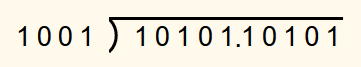About the calculator
This calculator can be used to divide 2 binary numbers. The numbers may be negative and have fractional digits.
If the solution has fractional digits, the calculation is terminated when the specified number of fractional digits has been reached and when every digit of the dividend has been taken into account for the calculation. If the calculation is terminated, it is always rounded down (in the case of positive binary numbers).
If both binary numbers have no fractional digits and if there is a 0 in the field for the number of fractional digits and if the dividend cannot be completely divided by the divisor, then a division with remainder is performed.
Divide binary numbers without fractional digits
As an example, 11010012 should be divided by 1012. 11010012 corresponds to 105 in the decimal system and 1012 corresponds to 5 in the decimal system.
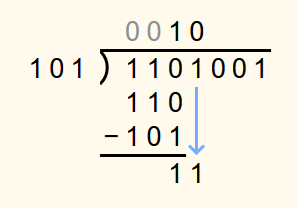
In principle, binary numbers can be divided in the same way as decimal numbers. First, the task is written down:
In each step of the calculation, one digit of the dividend is brought down. It starts with the leftmost digit. In the first step, the digit is written under the first digit of the dividend. In the following steps, it is appended to the number in the currently bottommost row in the calculation. If the number in the currently bottommost row is then smaller than the divisor, a 0 is appended to the solution. Otherwise, a 1 is appended to the solution and the divisor is subtracted from the number in the currently bottommost row. The digit that is appended to the solution is always written above the digit that was brought down in the current step.
In the example the first step is to write a 1 under the first digit of the dividend. As 12 is less than 1012, a 0 is entered in the solution row.
The second digit of the dividend is then appended to the number in the currently bottommost row. Since 112 is also less than 1012, a 0 is entered in the solution row again.
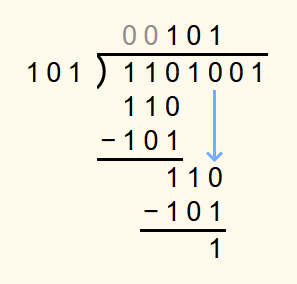
Next, the 0 is brought down. 1102 is not less than 1012 and so this time a 1 is appended to the solution and the divisor 1012 is subtracted from 1102.
In the next step, the 1 is brought down. As 112 is less than 1012, a 0 is appended to the solution.
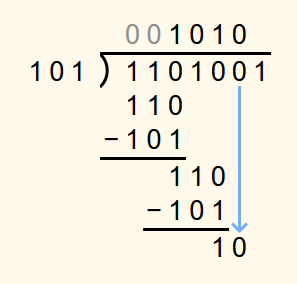
Then the 0 is brought down. 1102 is not less than 1012 and so a 1 is written in the solution row and 1012 is subtracted from 1102.
The next 0 is brought down. Since 102 is less than 1012, another 0 is appended to the solution.
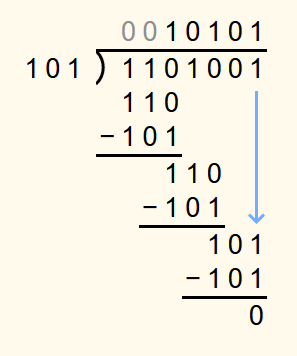
The 1 is then brought down. Since 1012 is not less than 1012, a 1 is appended to the solution and 1012 is subtracted from 1012.
Now each digit of the dividend has been brought down once and the number in the lowest row of the calculation is 0. Therefore, the exact result has been found. 101012 corresponds to 21 in the decimal system.
Solution with fractional digits
If all digits of the dividend have been "used up" and the bottommost number is not 0, then the solution has at least one fractional digit. In this case, a binary point is appended to both the solution and the dividend. Then, in each step, a 0 is appended to the dividend. This is brought down and, depending on whether the current bottommost number is smaller than the divisor or not, either a 0 is appended to the solution or a 1 is appended to the solution and the divisor is subtracted from the current bottommost number. This is repeated until either the bottommost number is 0 or until enough fractional digits have been calculated.
As an example, 10112 should be divided by 1002. 10112 corresponds to 11 in the decimal system and 1002 corresponds to 4 in the decimal system.
The calculation is performed until all digits of the dividend have been brought down once.
Since the bottommost number is not 0, a binary point is appended to both the dividend and the solution.
Then a 0 is appended to the dividend and brought down. Since 1102 is not less than 1002, a 1 is appended to the solution and 1002 is subtracted from 1102.
The bottommost number is still not 0. So another 0 is appended to the dividend and brought down. As 1002 is not less than 1002, another 1 is appended to the solution and 1002 is subtracted from 1002.
The bottommost number is now 0, so the exact solution has been found. 10.112 corresponds to 2.75 in the decimal system.
Divide binary numbers with remainder
If a division with remainder is to be performed for 2 binary numbers, the division is first performed as described above until all digits of the dividend have been used up. Then the bottommost number is the remainder.
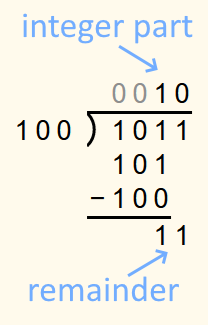
As an example, 10112 is to be divided by 1002 again.
The division is performed until all digits have been brought down once.
The bottommost number is the remainder. The solution is therefore 102 r 112.
Divide binary numbers with fractional digits
Dividend has fractional digits
If the dividend has fractional digits but the divisor does not, then the division is first performed as described above until all digits before the binary point have been processed. Then a binary point is appended to the solution and the calculation continues with the fractional digits. If all fractional digits have been processed but the bottommost number in the calculation is not 0, then in each step a 0 is appended to the dividend and to the bottommost number.
As an example, 100.112 should be divided by 102. 100.112 corresponds to 4.75 in the decimal system and 102 corresponds to 2 in the decimal system.
First, the calculation is performed until all the digits of the dividend before the binary point have been processed.
Then, a binary point is appended to the solution.
Next, the first digit after the binary point is appended to the bottommost number in the calculation. As 12 is less than 102, a 0 is appended to the solution.
The second digit after the binary point is then appended to the bottommost number. As 112 is not less than 102, a 1 is appended to the solution and 102 is subtracted from 112.
The bottommost number in the calculation is not 0, so the next step is to append a 0 to the bottommost number. As 102 is not less than 102, a 1 is appended to the solution and 102 is subtracted from the bottommost number.
Now the bottommost number is 0 and therefore the exact solution has been found. 10.0112 corresponds to 2.375 in the decimal system.
Divisor has fractional digits
If the divisor has fractional digits, these must first be eliminated. This is achieved by shifting the binary points of the dividend and the divisor to the right by as many places until the divisor no longer has any fractional digits.
For example, 101.01101012 should be divided by 10.012.
The divisor 10.012 has 2 fractional digits. This means that the binary point of both the dividend and the divisor is shifted 2 places to the right. The new dividend is therefore 10101.101012 and the new divisor is 10012.
The calculation is then performed.